Kuartil Data Tunggal

Kuartil ialah nilai-nilai yang membagi data yang telah diurutkan kedalam 4 bab yang sama besar. Kuartil dinotasikan dengan notasi $Q$. Kuartil terdiri dari 3, yaitu kuartil pertama $(Q_1),$ kuartil kedua $(Q_2),$ dan kuartil ketiga $(Q_3).$

Untuk memilih kuartil pada data tunggal, kita harus mempertimbangkan banyaknya data $(n)$ terlebih dahulu. Penghitungan kuartil tergantung dari kondisi banyaknya data tersebut.

Sebagai ilustrasi, misalkan terdapat seperangkat data yaitu $x_1, x_2, \cdots, x_n.$ Letak-letak kuartil pada data tersebut sanggup dilihat pada gambar di bawah ini.
Penentuan kuartil berdasarkan kondisi banyaknya data ialah sebagai berikut.

1. Kuartil untuk banyaknya data $(n)$ ganjil dan $n+1$ habis dibagi 4.


2. Kuartil untuk banyaknya data $(n)$ ganjil dan $n+1$ tidak habis dibagi 4.


3. Kuartil untuk banyaknya data $(n)$ genap dan habis dibagi 4.


4. Kuartil untuk banyaknya data $(n)$ genap dan tidak habis dibagi 4.

Rumus-rumus di atas sangat baik dipakai untuk jumlah data banyak. Untuk jumlah data yang kecil, penentuan kuartil lebih gampang ditentukan dengan piramida berikut ini.

1. Kuartil untuk jumlah data $(n)$ ganjil.


2. Kuartil untuk jumlah data (n) genap.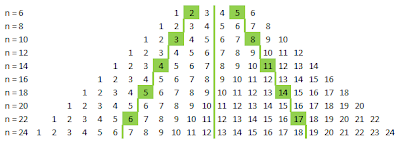


Jika kuartil terletak di antara dua nilai, maka nilai kuartil ialah rata-rata dari kedua nilai tersebut.

Contoh Soal No. 1

Berikut ini ialah data panjang jalan di sebuah kawasan dalam satuan kilometer.

5, 6, 7, 3, 2

Hitunglah kuartil dari data panjang jalan tersebut?

Jawab:

Karena jumlah data ialah ganjil dan tidak banyak, maka penghitungan kuartil memakai piramida kuartil untuk data ganjil.  Pada piramida tersebut, letak kuartil ialah sebagai berikut.

1. Kuartil 1 terletak antara data pertama dan kedua.
2. Kuartil 2 ialah data ketiga.
3. Kuartil 3 terletak antara data keempat dan kelima.

Sebelumnya data diurutkan terlebih dahulu menjadi sebagai berikut.

2, 3, 5, 6, 7

Kuartilnya ialah sebagai berikut.
Contoh Soal No. 2

Sepuluh orang mahasiswa sebuah perguruan tinggi tinggi dijadikan sampel dan dihitung tinggi badannya. Hasil pengukuran tinggi tubuh kesepuluh mahasiswa tersebut ialah sebagai berikut.

172, 167, 180, 171, 169, 160, 175, 173, 170

Tentukan nilai kuartil dari data tinggi tubuh mahasiswa tersebut!

Jawab:

Karena banyaknya data genap dan tidak banyak, maka penentuan kuartil sanggup memakai piramida kuartil data genap. Pada piramida tersebut, letak kuartil ialah sebagai berikut.

1. Kuartil 1 ialah data ketiga.
2. Kuartil 2 terletak antara data kelima dan keenam.
3. Kuartil 3 ialah data kedelapan.

Sebelumnya, data harus kita urutkan terlebih dahulu. Hasilnya ialah sebagai berikut: 160, 165, 167, 169, 170, 171, 172, 173, 175, 180. Dengan demikian, nilai-nilai kuatil ialah \begin{align*} Q_1 &= 167\\ Q_2 &= \frac{170+171}{2} = 170\text{,}5\\ Q_3 &= 173 \end{align*}
Contoh Soal No. 3

Jumlah data ialah 223. Tentukan letak kuartilnya!

Jawab:

Jumlah data ialah ganjil dan jikalau n ditambah 1, kesudahannya habis dibagi 4. Oleh alasannya ialah itu penentuan kuartil memakai kondisi pertama.
Contoh Soal No. 4

Jumlah data ialah 197. Tentukan letak kuartilnya!

Jawab:

Jumlah data ialah ganjil dan jikalau n ditambah 1, kesudahannya tidak habis dibagi 4. Oleh alasannya ialah itu penentuan kuartil memakai kondisi kedua.
Contoh Soal No. 5

Jumlah data 400. Tentukan letak kuartilnya!

Jawab:

Jumlah data ialah genap dan habis dibagi 4. Oleh alasannya ialah itu penentuan kuartil memakai kondisi ketiga.

Contoh Soal No. 6

Jumlah data 350. Tentukan letak kuartilnya!

Jawab:

Jumlah data ialah genap dan tidak habis dibagi 4. Oleh alasannya ialah itu penentuan kuartil memakai kondisi keempat.

{codeBox}